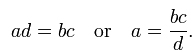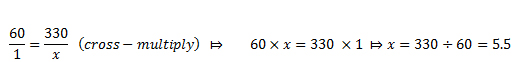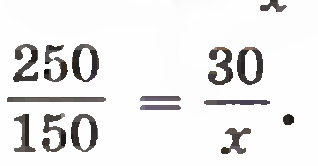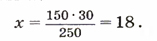In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, x and y are proportional if the ratio 
is constant. We also say that one of the quantities is proportional to the other. For example, if the speed of an object is constant, it travels a distance that is proportional to the travel time.
If a linear function transforms 0, a and b into 0, c and d, and if the product a b c d is not zero, we say a and b are proportional to c and d. An equality of two ratios such as 
where no term is zero, is called a proportion.
In mathematics, specifically in elementary arithmetic and elementary algebra, given an equation between two fractions or rational expressions, one can cross-multiply to simplify the equation or determine the value of a variable.
For an equation like the following:
one can cross-multiply to get:
Problem 1:
If a secretary types 60 words per minutes, how many minutes will he take to type 330 words ?
Solution:
We must distinguish between problems with direct and inverse variations.
Problem 2 :
Tea is packaged in 39 packs of 150 grams each. How many packs we will get if the same amount of tea is packaged in packs of 250 grams?
Solution:
Lets take by the x number of packs of 250 grams of tea and a brief statement of the problem can be written:
150 g – 30 packs
250 g – x packs.
Number of packs of tea is inversely proportional weight of a pack: how many times will increase the mass of the pack, the same factor will decrease the number of packets. . Now you have to create an equal ratios. It is important not to be a fool here: the ratio of 
will not equal 
, but the inverse ratio of 
;
We will get proportion:
Then 
When you see a ratio – such as a : b. If it is not a part -to part ratio, then just think it as a fraction. For instance, 5:6 = 5/6. If it is part to part ratio, just divide each number by the sum to find the fraction of each part to the whole. For instance, if the ratio of boys to girls in a class is 5:6, then the sum is 5+6= 11, so the boys make up 5/11 of the whole class, and the girls make up 6/11 of the whole class.
Proportional division
Problem 3
The three firms have invested in some project, respectively, 6, 4 and 2 million dollars. And got 24 million profit. How should they split the profit?
Usually assumed that the distribution of profits must comply shares funds contributed to the project by investors. In such cases, they write one long ratio: 6:4:2.
So the distributions of the profit should be shared following this ratio. In such cases, write one long ratio: 6: 4: 2.
Our arguments have brought us to a familiar problem.
In total there are 6 +4 +2 = 12 parts, so each part has to 24 : 12 = 2.
Consequently, the first company to get a 2 x 6 = 12, second- 4 x 2=8, third – 2 x 2 = 4 million dollars.
Note that considering the ratio of 6 : 4 : 2 for the problem could be reduced, i. e., divided by each of numbers on their common factor which is the number 2.
