A segment, ray, line or palne that is perpemndicular to a segment at its midpoint is called a perpendicular bisector.
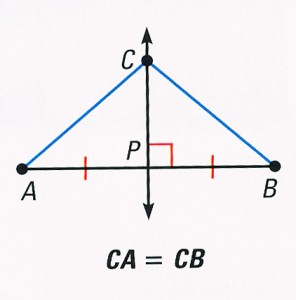
Theorem 1.1 Perpendicular Bisector Theorem
If a point is on perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment.
If CP is the perpendicular bisector of AB, then CA = CB
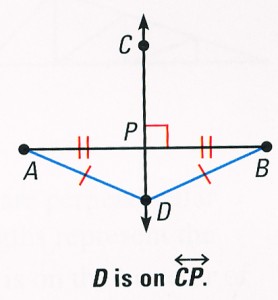
Theorem 1.2 Converse of the Perpendicular Bisector Theorem
If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment.
If DA = DB, then D lies on the perpendicular bisector of AB.
Definition: The distance from a point to a line is define as the length of the perpendicular segment from the point to the line.
Definition: When a pint is the same distance from one line as it is from another line, then the point is equidistant from the two lines.
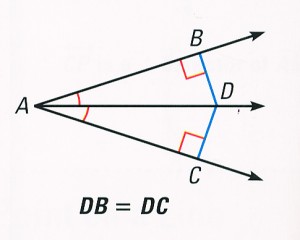
Theorem 2.1 Angle Bisector Theorem
If a point is on the bisector of an anlgle, then it is equidistant from the two sides of the angle.
If ∠BAD = ∠CAD, then DB = DC.
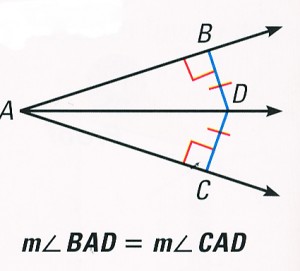
Theorem 2.2 Converse of the Angle Bisector Theorem
If a point is in the interior of an angle and is equidistant from the sides of the angle, then it lies on the bisector of the angle.
If DB = DC, then ∠BAD = ∠CAD
Definition: When three or more lines intersect in the same point, they are called concurrent lines. The point of intersection of lines is called the point of concurrency.
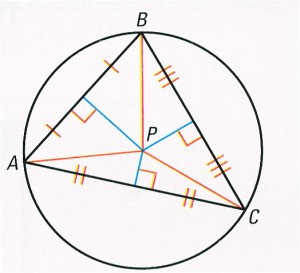
Definition: The point of concurrency of the perpendicular bisectors of triangles is called the circumcenter of the triangle.
Theorem 3.1 Concurrency of Perpendicular Bisectors of a Triangle
The perpendicular bisector of a triangle intersect at a point that is equidistant from the vertices of the triangle.
PA = PB = PC
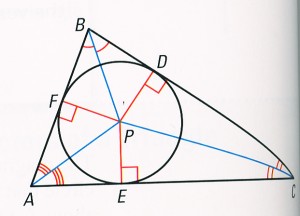
Definition: The point of concurrency of the angle bisectors is called the incentsr of the triangle and it always lies inside the triangle.
Theorem 4.1 Concurrency of Perpendicular Bisectors of a Triangle
The angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle.
PD = PE = PF
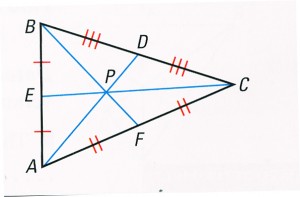
Definition: A median of a triangle is a segment whose endpoints are a vertex of the triangle and the midpoint of the opposite side.
Definition: The point of concurrency of the medians is called the centroid of the triangle. The centroid is always inside the triangle.
Theorem 5.1 Concurrency of Medians of a Triangle
The medians of a triangle intresect at a point that is two third of distance from each vertex to the midpoint of the opposite side.
If P is the centroid of ΔABC, then
AP= 2/3 AD, BP = 2/3 BF, CP = 2/3 CE
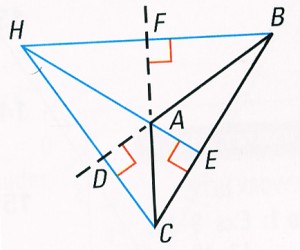
Definition: An altitude of a triangle is a perpendicular segment from vertex to the opposite side or the line that contains the opposite side.
Definition: The point of concurrency of the altitudes called the orthocenter of the triangle.
Theorem 6.1 Concurrency of Altitudes of a Triangle
The lines containing the altitudes of a triangle are concurrent.
If AE, BF and CD are altitudes of ΔABC, then the lines AE, BF and CD intersect at some point H.